Unraveling the Aho-Corasick String Matching Algorithm

The other day, I stumbled upon this algorithm and was truly captivated by its brilliance. I couldn’t resist the urge to share it with all of you, so here it is.

A bit of historical background

The Aho-Corasick algorithm (hereinafter “A-C”) was conceived by Alfred V. Aho and Margaret J. Corasick. A-C was introduced in their seminal paper titled “Efficient string matching: An aid to bibliographic search,” published in 1975. This work was aimed at addressing the computational challenges associated with bibliographic search, which is a crucial aspect of academic research and literary work management.

During the 1970s, bibliographic search was emerging as a critical challenge, especially with the burgeoning volume of academic literature. The need for efficient string matching algorithms was glaring, as traditional approaches were notably inefficient when tasked with searching for multiple patterns within large text corpora.

A-C is built upon earlier theoretical work in automata theory and the theory of computation. It leverages the power of trie data structures and finite automata to perform efficient string matching. The algorithm’s elegance lies in its simplicity and efficiency, making a single pass over the text, regardless of the number of patterns.

The Trie Structure

The journey begins with a data structure known as Trie, a type of search tree used to store a collection of strings. Each node in this tree represents a character, and a path from the root to a node spells out a word. This structure serves as the backbone of our algorithm, providing a map for the patterns we seek.

Constructing the Trie

Given a set of words, say {"he", "she", "his", "hers"}, the algorithm constructs a Trie. This process is akin to creating a directory where each word gets its own unique address based on its characters. As each word is processed, it’s broken down into individual characters which guide the formation of branches in the Trie. The commonality between the starting characters of different words is utilized to create shared branches, thus optimizing the structure.

For example, the words “he” and “hers” both start with the character ‘h’, so they share the initial branch. As we move to the next character, new branches are formed to accommodate the differences. This setup ensures that each word has a unique path within the Trie, yet common prefixes are represented efficiently.

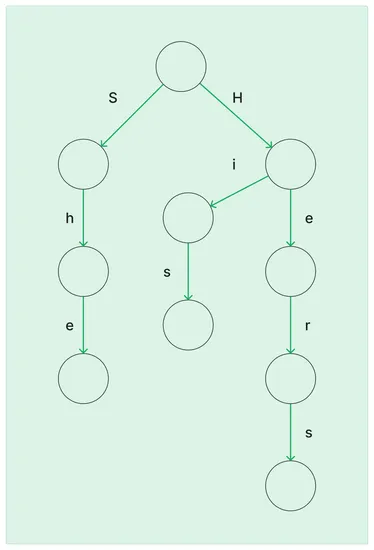
Crafting Failure Links

The algorithm then adorns the Trie with failure links, a mechanism to gracefully retreat and advance along different branches when a mismatch occurs. These links conect nodes in a manner that encapsulates the shared prefixes among the words, creating a network of fallbacks. It’s akin to having secret passages that swiftly guide the search to the right path upon encountering a hurdle.

The Search Begins

With a well-prepared Trie, the search commences. As the algorithm traverses the text, it follows the branches of the Trie, character by character. Each match propels it deeper into the Trie, while a mismatch ushers it along the failure links to the next potential matching position. This dance continues, seamlessly transitioning between the text and the Trie, leaving no stone unturned.

Harvesting the Matches

Whenever the traversal reaches the end of a word in the Trie, a match is found! The position of the match within the text is recorded, and the search marches on unfazed, in pursuit of other patterns.

The result

At the conclusion of this expedition, the algorithm presents a comprehensive list of all ocurrences of the words within the text. A-C’s ability to find multiple patterns in a single pass makes it a cherished asset in the toolbox of text processing.

Implementation

For those desiring a more tangible grasp, here is a TypeScript implementation of the Aho-Corasick algorithm.

We will start by defining the max number of states in buildMatchingMachine and the max number of characters in the alphabet.

const MAX_STATES = 500
const MAX_CHARS = 26

Next we will define the AhoCorasick class, which will be responsible for constructing the Trie and performing the search.

class AhoCorasick {
  private out: number[] = new Array(MAX_STATES).fill(0)
  private f: number[] = new Array(MAX_STATES).fill(-1)
  private g: number[][] = new Array(MAX_STATES)
    .fill(null)
    .map(() => new Array(MAX_CHARS).fill(-1))

  constructor(private keywords: string[]) {}

  /**
   * Builds the Aho-Corasick machine, initializing the goto, failure,
   * and output functions.
   * @returns The total number of states in the machine.
   */

  private buildMatchingMachine(): number {
    this.out.fill(0)
    this.g = new Array(MAX_STATES)
      .fill(null)
      .map(() => new Array(MAX_CHARS).fill(-1))

    let states = 1

    for (let i = 0; i < this.keywords.length; ++i) {
      const word = this.keywords[i]
      let currentState = 0

      for (let j = 0; j < word.length; ++j) {
        const ch = word.charCodeAt(j) - 'a'.charCodeAt(0)

        if (this.g[currentState][ch] === -1) {
          this.g[currentState][ch] = states++
        }

        currentState = this.g[currentState][ch]
      }

      this.out[currentState] |= 1 << i
    }

    for (let ch = 0; ch < MAX_CHARS; ++ch) {
      if (this.g[0][ch] === -1) {
        this.g[0][ch] = 0
      }
    }

    this.f.fill(-1)

    const q: number[] = []
    for (let ch = 0; ch < MAX_CHARS; ++ch) {
      if (this.g[0][ch] !== 0) {
        this.f[this.g[0][ch]] = 0
        q.push(this.g[0][ch])
      }
    }

    while (q.length) {
      const state = q.shift()!

      for (let ch = 0; ch < 26; ++ch) {
        if (this.g[state][ch] !== -1) {
          let failure = this.f[state]

          while (this.g[failure][ch] === -1) {
            failure = this.f[failure]
          }

          failure = this.g[failure][ch]
          this.f[this.g[state][ch]] = failure

          this.out[this.g[state][ch]] |= this.out[failure]

          q.push(this.g[state][ch])
        }
      }
    }

    return states
  }

  /**
   * Finds the next state based on the current state and the next input character.
   * @param currentState - The current state in the machine.
   * @param nextInput - The next input character.
   * @returns The next state in the machine.
   */

  private findNextState(currentState: number, nextInput: string): number {
    let answer = currentState
    const ch = nextInput.charCodeAt(0) - 'a'.charCodeAt(0)

    while (this.g[answer][ch] === -1) {
      answer = this.f[answer]
    }

    return this.g[answer][ch]
  }

  /**
   * Searches for all occurrences of the keywords in the given text.
   * @param text - The text to search.
   */

  public searchWords(text: string): void {
    if (!text) {
      console.log('The text to search cannot be empty or null.')
      return
    }

    this.buildMatchingMachine()

    let currentState = 0

    for (let i = 0; i < text.length; ++i) {
      currentState = this.findNextState(currentState, text[i])

      if (this.out[currentState] === 0) continue

      for (let j = 0; j < this.keywords.length; ++j) {
        if (this.out[currentState] & (1 << j)) {
          console.log(
            `Word ${this.keywords[j]} appears from ${
              i - this.keywords[j].length + 1
            } to ${i}`,
          )
        }
      }
    }
  }
}

And finally we will use the class to search for the words in a given text.

const arr = ['he', 'she', 'hers', 'his', 'a']
const text = 'ahishers'
const ahoCorasickMachine = new AhoCorasick(arr)
ahoCorasickMachine.searchWords(text)

// Output:
// Word his appears from 1 to 3
// Word he appears from 4 to 5
// Word she appears from 3 to 5
// Word hers appears from 4 to 7